Here are some examples we have come up with so far. Please email any of us on the project Greg Balco, Ben Laabs, and/or Joe Tulenko with your ideas so we can add them to the list!

---

1) Data-model comparison between LGM and penultimate moraine ages, and model output from simulations over multiple glaciations (ie the ice sheet influence on regional climate example). Hypothesis: if the impact from ice sheets on re-arranging large-scale atmospheric circulation and thus modulating regional climate is actually significant, we should be able to use climate model output to predict the geospatial patterns of moraine preservation over multiple glacial cycles. This could be tested by comparing moraine ages and geospatial patterns from the database with model output to see where there is good fit between model output and data and where there isn't.

See the example output figure below and find a link to the tutorial here.

---

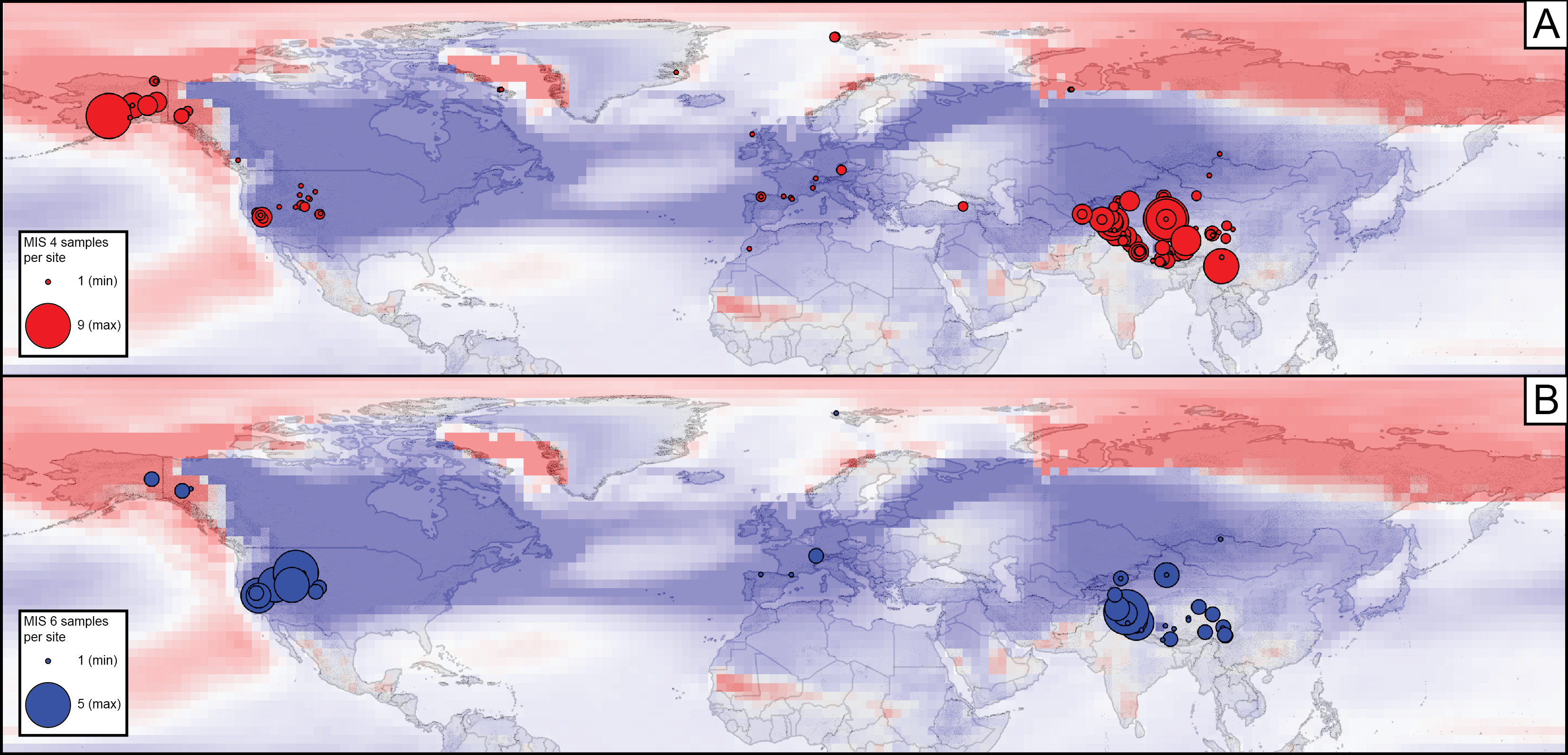
2) Testing global expression of Younger Dryas Please find a tutorial and some matlab scripts used to generate some of the plots found in a recent paper from Greg Balco (Balco, 2021) in this example.

Tutorial here.

Matlab scripts here in this zipped folder.

---

3) Post-Glacial Greenland ice-sheet retreat time-distance diagram following up on a workshop at the University at Buffalo, we attempt to generate a time-distance diagram of SW Greenland Ice Sheet retreat and you can find the matlab script here to generate the following results:

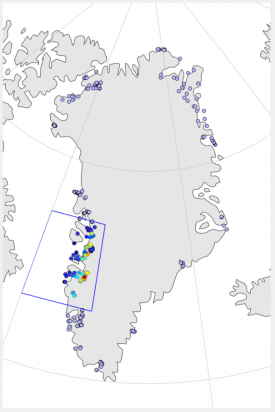
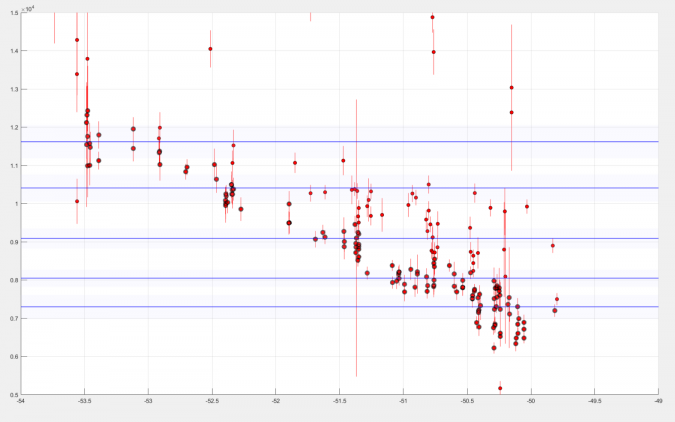
The script combs through the new database and selects all ages from 'boulder' samples specifically from ICE-D Greenland that exist within the bounds box on the first figure and then plots the ages against longitude to convincingly show that as you move from the coast inland, ages generally get younger and track the recession of the Greenland Ice Sheet through the Holocene.

% Does deglaciation TDD for west Greenland....
clear all; close all;

%% For MAC users use this set of code to connect to the database
% First set up SSH tunnel on port 12345.
%dbc = database('iced','reader','beryllium-10','Vendor','MySQL','server','localhost','port',12345);

%% For WINDOWS users use this set of code to connect to the database
dbc = database('ICED2', 'reader', 'beryllium-10');

%% get all samples

q1 = ['select iced.base_sample.lat_DD, iced.base_sample.lon_DD ' ...
    'from iced.base_sample,iced.base_application_sites,iced.base_application ' ...
    'where iced.base_sample.site_id = iced.base_application_sites.site_id ' ...
    'and iced.base_application_sites.application_id = iced.base_application.id ' ...
    'and iced.base_application.Name = "Greenland"'];

result1 = fetch(dbc,q1);

%% get West Greenland samples

blats = [64.8 71];
%blats = [61 71];
blons = [-60 -48];

q2 = ['select iced.base_sample.lat_DD, iced.base_sample.lon_DD ' ...
    ' from iced.base_sample,iced.base_application_sites,iced.base_application ' ...
    ' where iced.base_sample.lat_DD < ' sprintf('%0.1f',blats(2)) ...
    ' and iced.base_sample.lon_DD < ' sprintf('%0.1f',blons(2)) ...
    ' and iced.base_sample.lat_DD > ' sprintf('%0.1f',blats(1)) ...
    ' and iced.base_sample.lon_DD > ' sprintf('%0.1f',blons(1)) ...
    ' and iced.base_sample.site_id = iced.base_application_sites.site_id ' ...
    ' and iced.base_application_sites.application_id = iced.base_application.id ' ...
    ' and iced.base_application.Name = "Greenland"'];

result2 = fetch(dbc,q2);

locs1 = cell2mat(table2cell(result1));
locs2 = cell2mat(table2cell(result2));

%% get age data from everything

q3 = ['select iced.base_sample.lat_DD, iced.base_sample.lon_DD, ' ...
    'iced.base_calculatedages.t_St,iced.base_calculatedages.t_LSDn,iced.base_calculatedages.dtint_St, ' ...
    'iced.base_calculatedages.dtext_St ' ...
    'from iced.base_sample, iced.base_calculatedages, iced.base_application_sites,iced.base_application' ...
    ' where iced.base_sample.id = iced.base_calculatedages.sample_unique_id ' ...
    ' and iced.base_sample.site_id = iced.base_application_sites.site_id ' ...
    ' and iced.base_application_sites.application_id = iced.base_application.id ' ...
    ' and iced.base_application.Name = "Greenland"' ...
    ' and lat_DD < ' sprintf('%0.1f',blats(2)) ' and lon_DD < ' sprintf('%0.1f',blons(2)) ' and lat_DD > ' sprintf('%0.1f',blats(1)) ' and lon_DD > ' sprintf('%0.1f',blons(1))];

result3 = fetch(dbc,q3);

%% 

ages1 = cell2mat(table2cell(result3));

% And just from boulders
q4 = [q3 ' and iced.base_sample.what like "%boulder"'];

result4 = fetch(dbc,q4);

ages2 = cell2mat(table2cell(result4));

close(dbc);

%% 

figure(1); clf; 
% Center on Greenland Summit
gisplat = 72 + 36/60;
gisplon = -38.5;

xl = [-0.18 0.15];
yl = [-0.25 0.25];

tx = xl(1) + 0.95*diff(xl);
ty = yl(1) + 0.06*diff(yl);
ts = 14;

mw = 0.005;
awx = (1 - 5*mw)/4;
awy = (1-2*mw);

axesm('mapprojection','eqdazim','origin',[gisplat gisplon 0]);

%axesm('globe','grid','on')


g1 = geoshow('landareas.shp');
set(get(g1,'children'),'facecolor',[0.9 0.9 0.9]);
set(gca,'xlim',xl); 
set(gca,'ylim',yl);
hold on;


% Plot all samples
plotm(locs1(:,1),locs1(:,2),'ko','markerfacecolor',[0.7 0.7 1]);
% Plot only samples in west greenland selection box
plotm(locs2(:,1),locs2(:,2),'ko','markerfacecolor',[0.2 0.2 1]);


plotm(blats([1 1 2 2 1]),blons([1 2 2 1 1]),'b','linewidth',1);



%

set(gca,'box','off','xcolor',[1 1 1],'ycolor',[1 1 1]);
%plotm(gisplat,gisplon,'ko','markerfacecolor','w');
%text(tx,ty,[sprintf('%0.0f',100*f2) '%'],'fontsize',ts,'horizontalalignment','right');

hg = gridm('on');
set(hg,'clipping','on');
set(hg,'linestyle','-','color',[0.75 0.75 0.75]);

temp = jet(12);
for a = 1:12
    maxage = 11000 - (a-1).*500;
    minage = maxage - 500;
    these = find(ages2(:,3) < maxage & ages2(:,3) > minage);
    if length(these) > 0
        plotm(ages2(these,1),ages2(these,2),'o','color',[0.5 0.5 0.5],'markerfacecolor',temp(a,:));drawnow;
    end
end





%% Plot

figure(2); clf; 
%plot(ages1(:,2),ages1(:,3),'bo','markerfacecolor',[0.5 0.5 1]);
hold on;

for a = 1:size(ages2,1)
    xx = [1 1].*ages2(a,2);
    yy = ages2(a,3) + [-1 1].*ages2(a,5);
    plot(xx,yy,'r'); hold on;
end

plot(ages2(:,2),ages2(:,3),'ko','markerfacecolor','r');
set(gca,'ylim',[5000 15000]); grid on;

%% Plot proposed cold periods from Young and others, etc. 

hold on;

events = [11620 10410 9090 8050 7300];
devents = [430 350 260 220 310];

for a = 1:length(events)
    xx = [-54 -49]; yy = [events(a) events(a)];
    plot(xx,yy,'b','linewidth',1);
    xx = [-54 -49 -49 -54 -54];
    yy = [events(a)-devents(a) events(a)-devents(a) events(a)+devents(a) events(a)+devents(a) events(a)-devents(a)];
    patch(xx,yy,[0.8 0.8 1],'edgecolor','none','facealpha',0.1);
end
 
%% filter for better AEP performance
p1 = polyfit([-53.5 -49.88],[11500 6426],1);
px = [-54 -49]; py = polyval(p1,px); %plot(px,py,'g');

predt = polyval(p1,ages2(:,2));
okclip = find(abs(predt - ages2(:,3)) < 1000);
plot(ages2(okclip,2), ages2(okclip,3),'ko','markersize',8);

aept = ages2(okclip,3);
aepdt = ages2(okclip,5);
aepz = -ages2(okclip,2).*100 - 4900;

% Get bounding curve

out = aep_bound(aept,aepz,0);
figure(2);
aept_out = out.t; aepx_out = -(out.z + 4900)./100;
plot(aepx_out,aept_out,'k'); 

%% MCS bounding curve

% Interestingly, this is weirdly pathological because at the westings where
% there are a lot of data, almost all the random iterations have one
% outlier that pulls it out. So it actually doesn't really work. 

if 1

figure; 
plot(aept,aepz,'ro'); hold on; drawnow;
p1 = plot(1000,1000,'ro');
ni = 100;
intt = 6500:10:12000;
for a = 1:ni
    thist = randn(size(aept)).*aepdt + aept;
    thisz = aepz;
    out = aep_bound(thist,thisz,0);
    delete(p1);
    p1 = plot(thist,thisz,'bo');
    plot(out.t,out.z,'k'); drawnow; pause;
    %inty(a,:) = interp1(out.t,out.z,intt);
    %plot(intt,inty(a,:),'k');
    disp(a);
end

end
    
%% 

if 1
    
    % Make figure comparing this to Holocene "events" 

    figure;
    diffx = diff(aepx_out)./diff(aept_out);
    for a = 1:length(diffx)
        xx = [aept_out(a) aept_out(a+1) aept_out(a+1)];
        if a == length(diffx)
            yy = -[diffx(a) diffx(a) diffx(a)];
        else
            yy = -[diffx(a) diffx(a) diffx(a+1)];
        end
        plot(xx,yy,'r'); hold on;
    end


    set(gca,'xlim',[6000 12000]);
    grid on;
    for a = 1:length(events)
        yy = [0 5e-3]; xx = [events(a) events(a)];
        plot(xx,yy,'b','linewidth',1);
        yy = [0 5e-3 5e-3 0 0];
        xx = [events(a)-devents(a) events(a)-devents(a) events(a)+devents(a) events(a)+devents(a) events(a)-devents(a)];
        patch(xx,yy,[0.8 0.8 1],'edgecolor','none','facealpha',0.1);
    end
    
end

---

4) Determining if measurement precision has gotten better through time This is a somewhat simple and fun exercise to investigate whether or not we as a community have been making progressively better measurements (ie improvements to field sample techniques, lab extraction procedures, AMS measurements, etc that should hopefully be leading to more precise cosmo measurements).

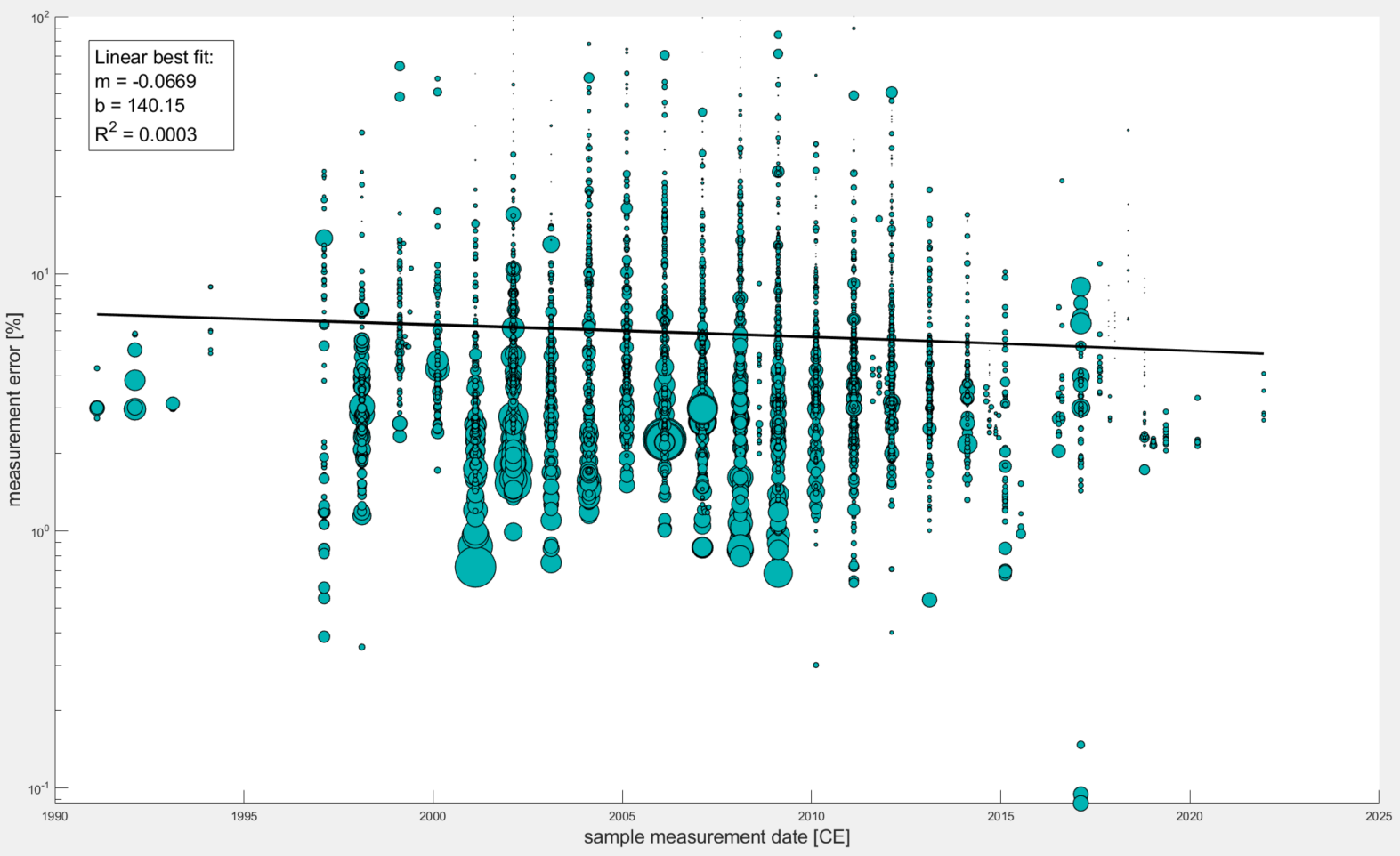
See the summary plots below that show the story is a bit more complicated; essentially one must remove the effect of sample concentration on sample percent error.

Plot One This is what you get when you plot measurement errors (%) for all samples in the database (with sample collection dates) against their sample collection dates. There is a linear trend fitted to the data with a very poor R^2 value.

Plot 2 As it should be obvious from the plot, there is a notable power relationship between sample concentration and percent error. This should make sense because the higher the concentration of Be-10 in the sample, the smaller % of that is from background Be-10 (ie Be-10 that was not originally trapped within sample quartz grains but was rather either from meteoric Be-10 that contaminated samples, Boron contamination that has the same atomic mass as Be-10, and/or Be-10 that came with the Be-9 carrier).

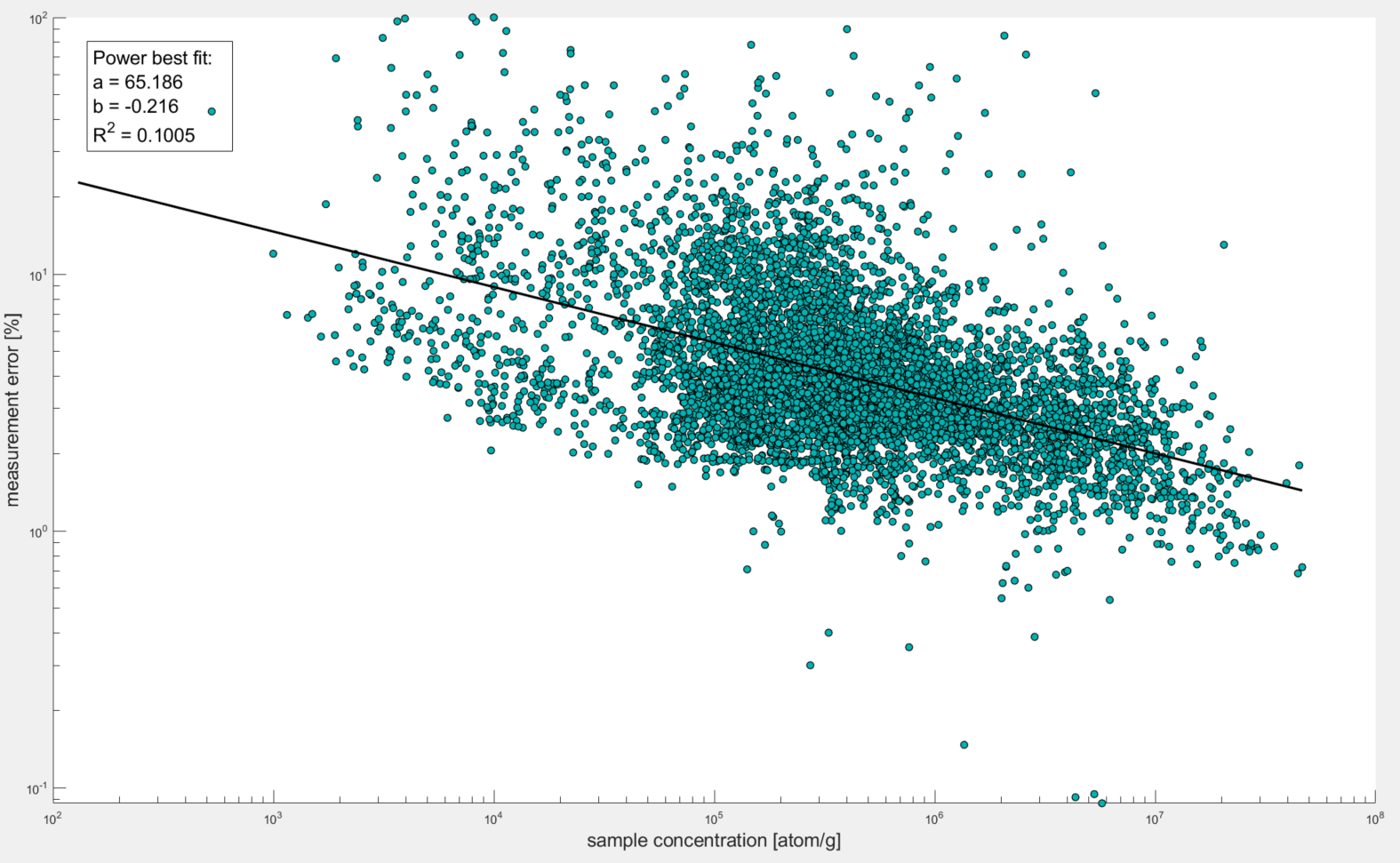
Plot 3 So what we need to do is detrend the data based on this power relationship. An easy way to do this is to simply calculate an expected value (based on the power relationship) and subtract that expected value from the observed measurement error. I could have made another plot to demonstrate this, but essentially if you plot detrended measurement errors against sample concentrations, the trendline you could fit to the data will be horizontal and centered at zero.

The final plot below shows what happens when you plot detrended measurement errors against sample collection date. Notice that the R^2 value is still relatively low but did increase by a factor of 4 and the slope became slightly more negative. Maybe this very loose correlation does say something about community improvement… What do you think?

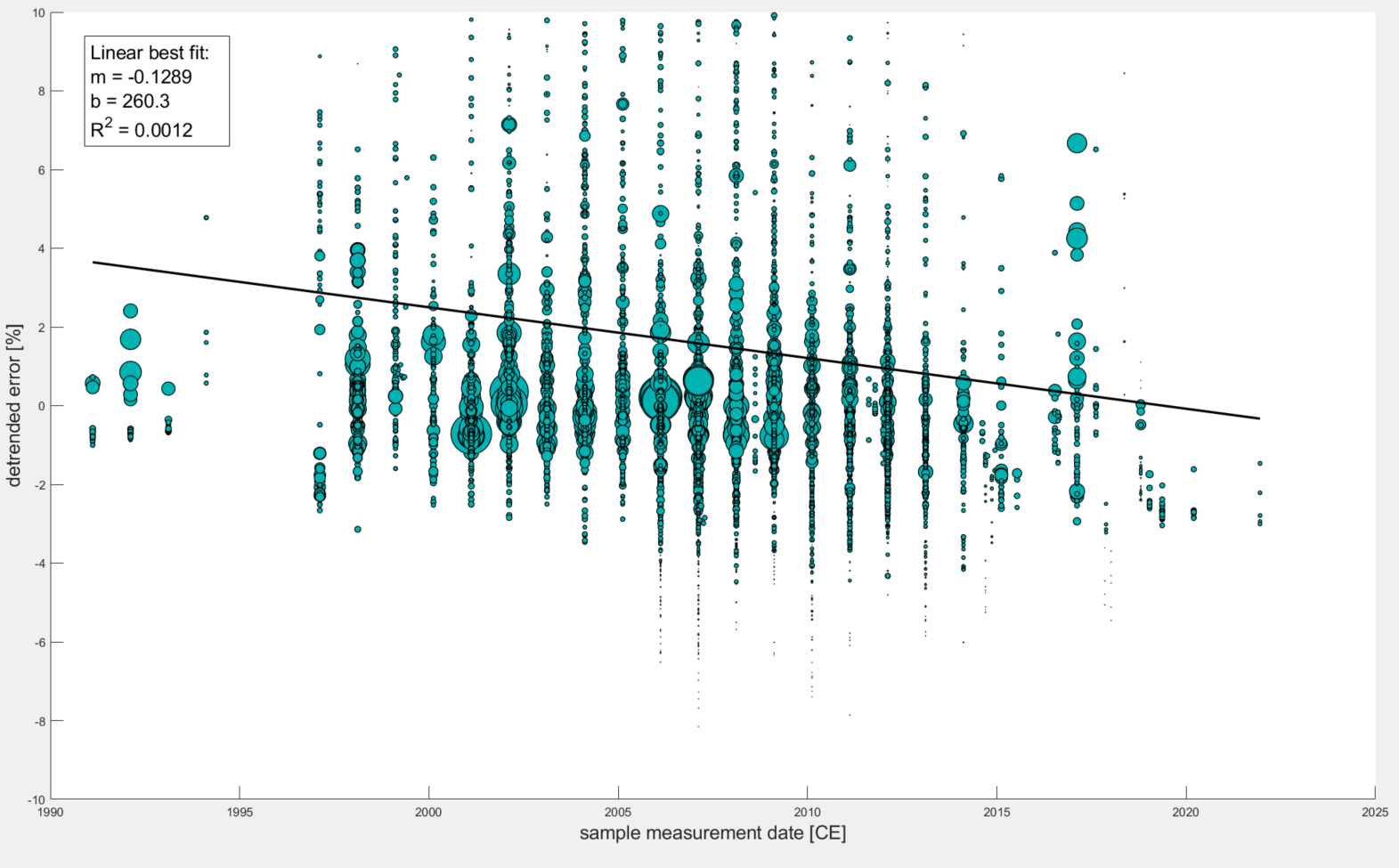
and the code to make these plots is below:

%%%% A matlab script for extracting all 10Be measurements from the alpine/entire database that have sample collection date info
%%%% and plotting their % measurement uncertainty against collection date
%%%% to see if we collectively as a community have gotten any better over the years 
%%%% at making these measurements. Largest improvements I would expect
%%%% should come from laboratory procedures (ie lower level blanks, better
%%%% 10Be isolation techniques, AMS precision improvement (maybe), etc.

%clear out all pre-existing variables and windows to start fresh
clear all; close all;

% as always, one must first connect to ICE-D. 
% Before running the script, be sure that you are connected to ICE-D in
% Heidi SQL!
% The script for connecting from a windows OS is as follows,
% assuming you set up an ODBC connection:

dbc = database('ICED2','reader','beryllium-10');

% here is some code from Greg Balco for connecting to the database from a
% Mac computer. I have no idea if it actually works but here it is for
% y'all.

% Get Sequel Pro running and use
% the below to find the SSH tunnel port. 

%[sys1,sys2] = system('ps aux | grep 3306');
%portindex = strfind(sys2,':173.194.241.211:');
%portstr = sys2((portindex(1)-5):(portindex(1)-1));


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Once connected to ICE-D, we want to extract ALL samples from the database
% that have sample collection date information found in the 'samples' tab.
% here is an SQL query formatted in matlab to extract all samples and
% format the sample names, date collected, concentration of 10Be atoms and
% AMS measurement error into one table:

%% Query to extract all 10Be data from the alpine database

q1 = ['select iced.base_sample.name, iced.base_sample.date_collected, iced._be10_al26_quartz.N10_atoms_g, iced._be10_al26_quartz.delN10_atoms_g, iced.base_calculatedages.t_LSDn ' ...
    ' from iced.base_sample, iced._be10_al26_quartz, iced.base_calculatedages, iced.base_site, iced.base_application_sites ' ...
    ' where iced.base_sample.id = iced._be10_al26_quartz.sample_id ' ...
    ' and iced.base_sample.id = iced.base_calculatedages.sample_unique_id ' ...
    ' and iced.base_sample.site_id = iced.base_site.id ' ...
    ' and iced.base_site.id = iced.base_application_sites.site_id ' ...
    ' and iced.base_sample.date_collected is not null ' ...
    ' and iced._be10_al26_quartz.N10_atoms_g is not null ' ...
    ' and iced._be10_al26_quartz.delN10_atoms_g is not null ' ...
    ' and iced.base_sample.date_collected not like "0000-00-00" ' ...
    ' and iced.base_sample.date_collected not like "0001-01-12" ' ...
    ' and iced.base_application_sites.application_id = 2 '];

%% If you would like to try the entire database (not just the alpine database) use this query instead of the first one

%q1 = ['select iced.base_sample.name, iced.base_sample.date_collected, iced._be10_al26_quartz.N10_atoms_g, iced._be10_al26_quartz.delN10_atoms_g, iced.base_calculatedages.t_LSDn ' ...
%    ' from iced.base_sample, iced._be10_al26_quartz, iced.base_calculatedages ' ...
%    ' where iced.base_sample.id = iced._be10_al26_quartz.sample_id ' ...
%    ' and iced.base_sample.id = iced.base_calculatedages.sample_unique_id ' ...
%    ' and iced.base_sample.date_collected is not null ' ...
%    ' and iced._be10_al26_quartz.N10_atoms_g is not null ' ...
%    ' and iced._be10_al26_quartz.delN10_atoms_g is not null ' ...
%    ' and iced.base_calculatedages.t_LSDn not like "0" ' ...
%    ' and iced.base_sample.date_collected not like "0000-00-00" ' ...
%    ' and iced.base_sample.date_collected not like "0001-01-12" '];

%% gather the data and organize it into cell arrays that can be used for plotting

% now, we want to store these selections as a table in matlab
% and convert the table into column vectors for plotting.
% this is made somewhat complicated by the fact that the dates extracted
% from ICE-D are in string format so you have to break them up.

samples.table = fetch(dbc,q1);
samples.date_cell = table2array(samples.table(:,2));
samples.date_cell_split = split(samples.date_cell,["-"]);
samples.date_raw = str2double(samples.date_cell_split);
samples.date_final = double(samples.date_raw(:,1) + (samples.date_raw(:, 2)/12) + (samples.date_raw(:,3)/30));
samples.conc = table2array(samples.table(:,3));
samples.err = table2array(samples.table(:,4));
samples.errpercent = double(((samples.err(:,1))./(samples.conc(:,1)))*100);
samples.age = table2array(samples.table(:,5));


% most important variables we created here are the samples.errpercent
% (sample error divided by sample concentration * 100), the final date
% collected (year + month/12 + day/30) and the age of each sample to make
% a scatterplot of percent error versus time (with marker size dictated by age)

%% Figure 1 - percent error by date measured without detrending the influence of sample concentration

fig1 = figure(1)
scatter(samples.date_final, samples.errpercent, 'filled',...
     'SizeData',(samples.age ./ 1000), 'MarkerEdgeColor',[0 0 0],...
     'MarkerFaceColor',[0 .7 .7],'LineWidth', 0.75)
ylim([0 100])
set(gca, 'YScale', 'log')
ylabel('measurement error [%]','FontSize',16)
xlabel('sample measurement date [CE]','FontSize',16)
dim1 = [.15 .9 0 0];
str1 = {['Linear best fit:'], ['m = -0.0669'], ['b = 140.15'], ...
    ['R^2 = 0.0003']};
annotation('textbox',dim1,'String',str1,'FitBoxToText','on', 'FontSize', 16);
hold on
x1 = samples.date_final;
y1 = -0.0669 * x1 + 140.15;
plot(x1,y1, "Color", [0 0 0],"LineStyle","-","LineWidth", 2)

% and that is the simple approach but as we know, there is a dependence 
% of precision on sample concentration (ie higher concentration = generally
% lower error since the background Be is less impactful for hot samples.
% to get around this, let's weigh each sample based on this relationship
% (see the script below and the resulting figure that demonstrates this 
% what-appears-to-be a power relationship.

%% Figure 2 establishing the relationship between sample concentration and percent error

fig2 = figure(2)
scatter(samples.conc, samples.errpercent, 'filled',...
     'MarkerEdgeColor',[0 0 0],...
     'MarkerFaceColor',[0 .7 .7],'LineWidth', 0.75)
ylim([0 100])
set(gca, 'Yscale', 'log', 'Xscale', 'log')
ylabel('measurement error [%]','FontSize',16)
xlabel('sample concentration [atom/g]','FontSize',16)
dim2 = [.15 .9 0 0];
str2 = {['Power best fit:'], ['a = 65.186'], ['b = -0.216'], ...
    ['R^2 = 0.1005']};
annotation('textbox',dim2,'String',str2,'FitBoxToText','on', 'FontSize', 16);
hold on
x2= samples.conc;
y2=65.185 * x2.^-0.216;
plot(x2,y2, "Color", [0 0 0],"LineStyle","-","LineWidth", 2)


% so now, let's plot percent errors weighted by the equation fit to 
% the precision vs concentration plot above. Simplest way to do this is to 
%detrend the data (ie generate a curve of expected values given the
%distribution - the fitted power curve - and subtract the expected values
%from the actual measurements. Then, plot the difference against the
%measurement date to remove the influence of sample concentration on error
%percent since we only want to know if error percent is decreasing over
%time.

%the way I have been thinking of it is like this: if we made the same
%measurement on the same exact sample every time (ie the expected
%concentration should be the same every time) for the past 30 years, and if
%we actually have been making better measurements, we should still see a
%decreasing trend in percent error over time (even though it is the exact
%same sample that we are measuring every time). Obviously this is not true,
%we've been making all sorts of measurements over the past 30 years and so
%this is an attempt to detrend the data in concentration vs percent error
%space and plot the detrended data against date of measurement. Anyway...

%% Figure 3 plotting percent error by date measured after accounting for influence of concentration on percent error

fig3 = figure(3)
y3 = samples.errpercent - y2;
scatter(samples.date_final, y3, 'filled',...
     'SizeData',(samples.age ./ 1000), 'MarkerEdgeColor',[0 0 0],...
     'MarkerFaceColor',[0 .7 .7],'LineWidth', 0.75)
ylim([-10 10])
ylabel('detrended error [%]','FontSize',16)
xlabel('sample measurement date [CE]','FontSize',16)
dim3 = [0.15 .9 0 0];
str3 = {['Linear best fit:'], ['m = -0.1289'], ['b = 260.3'], ...
    ['R^2 = 0.0012']};
annotation('textbox',dim3,'String',str3,'FitBoxToText','on', 'FontSize', 16);
hold on
x3= samples.date_final;
y3=-0.1289 * x3 + 260.3;
plot(x3,y3, "Color", [0 0 0],"LineStyle","-","LineWidth", 2)

---

5) Is there a correlation between Al/Be ratios and sample elevation? This example is based off a recent publication (Halsted et al., 2021) that found there is a correlation between Al / Be ratios and elevation that likely needs to be taken into account.

The resulting plot below demonstrates there is a negative correlation (ie the ratio decreases as elevation increases):

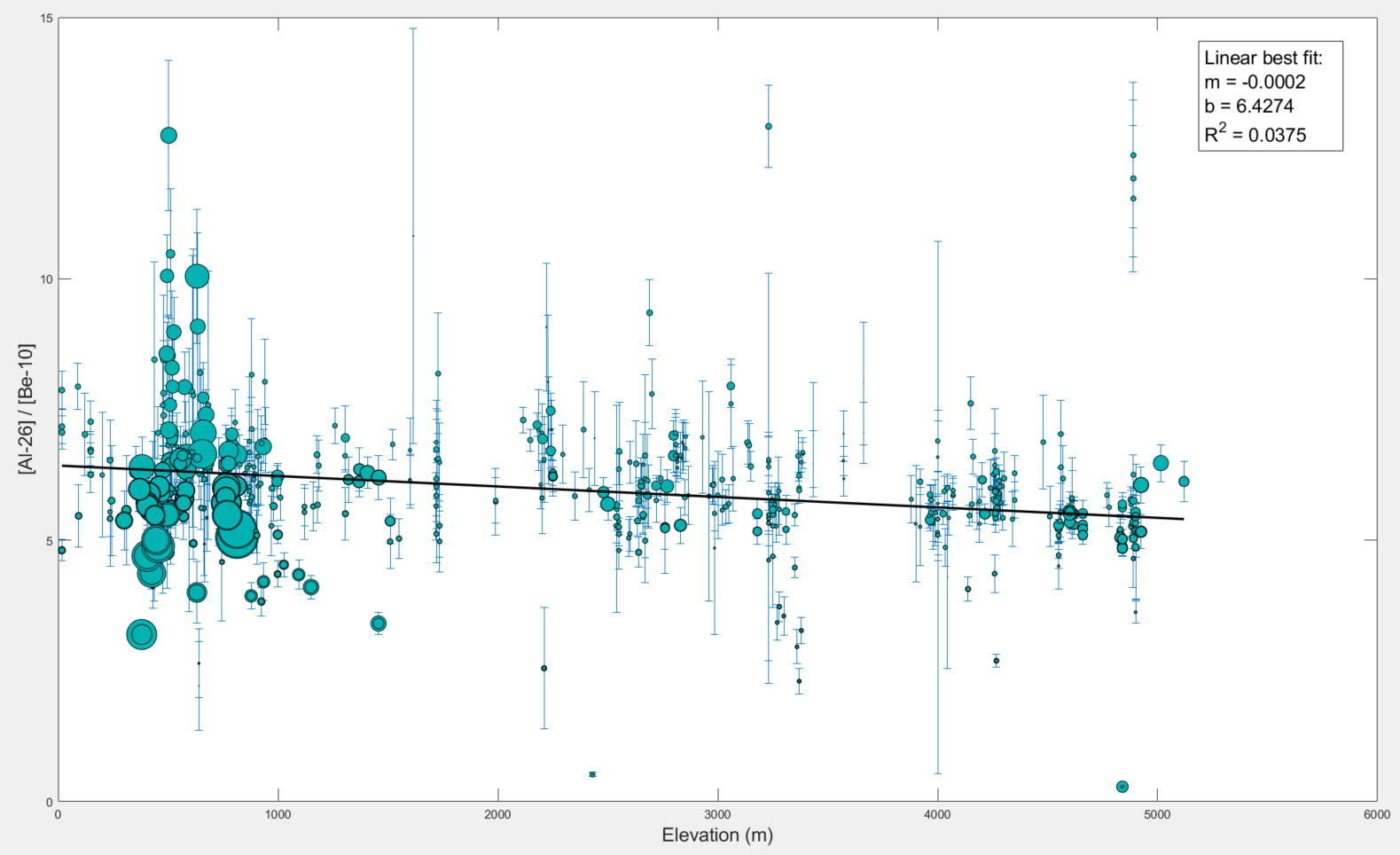
please find a script that you can copy into a new script editor written to produce this plot here.

% comparing the Al-Be ratio of all samples in the ICE-D alpine database
% against elevation to determine if there is an influence on the production
% and ratio of these two comsmogenic isotopes with elevation.

% clear out all pre-existing variables and windows to start fresh
clear all; close all;

% as always, one must first connect to ICE-D. 
% Before running the script, be sure that you are connected to ICE-D in
% Heidi SQL!
% The script for connecting from a windows OS is as follows,
% assuming you set up an ODBC connection:

dbc = database('ICED2','reader','beryllium-10');

% here is some code from Greg Balco for connecting to the database from a
% Mac computer. I have no idea if it actually works but here it is for
% y'all.

% Get Sequel Pro running and use
% the below to find the SSH tunnel port. 

%[sys1,sys2] = system('ps aux | grep 3306');
%portindex = strfind(sys2,':173.194.241.211:');
%portstr = sys2((portindex(1)-5):(portindex(1)-1));


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Once connected to ICE-D, we want to extract ALL samples from the database
% that have both Be-10 and Al-26 measurements and plot sample ratios
% against elevation.
% here is an SQL query formatted in matlab to extract all samples and
% format the sample names, Be-10 concentrations and errors, Al-26 concentrations
% and errors, sample elevations, and Be-10 exposure ages (to use for
% dictating marker size).

%% Query to extract all 10Be Al26 pairs from the alpine database

q1 = ['select iced.base_sample.name, ' ...
' iced.base_sample.elv_m, ' ...
' iced._be10_al26_quartz.N10_atoms_g, ' ...
' iced._be10_al26_quartz.delN10_atoms_g, ' ...
' iced._be10_al26_quartz.N26_atoms_g, ' ...
' iced._be10_al26_quartz.delN26_atoms_g, ' ...
' iced.base_calculatedages.t_LSDn ' ...
' from iced.base_sample, iced._be10_al26_quartz, iced.base_calculatedages, iced.base_site, iced.base_application_sites ' ...
' where iced.base_sample.id = iced._be10_al26_quartz.sample_id ' ...
' and iced.base_sample.id = iced.base_calculatedages.sample_unique_id ' ...
' AND iced.base_sample.site_id = iced.base_site.id ' ...
' and iced.base_site.id = iced.base_application_sites.site_id ' ...
' and iced.base_sample.elv_m is not NULL ' ...
' and iced._be10_al26_quartz.N10_atoms_g is not NULL ' ...
' and iced._be10_al26_quartz.N26_atoms_g is not null ' ...
' and iced._be10_al26_quartz.N26_atoms_g > 1000 ' ...
' and iced._be10_al26_quartz.N26_atoms_g not like 0 ' ...
' and iced.base_application_sites.application_id = 2 '];

%% If you would like to try the entire database (not just the alpine database) use this query instead of the first one
% Worth noting that in this query, we have not isolated the samples that
% have strictly simple exposure histories so there are probably a lot of
% samples in the dataset that are below the simple exposure ratio line

%q1 = ['select iced.base_sample.name, ' ...
%' iced.base_sample.elv_m, ' ...
%' iced._be10_al26_quartz.N10_atoms_g, ' ...
%' iced._be10_al26_quartz.delN10_atoms_g, ' ...
%' iced._be10_al26_quartz.N26_atoms_g, ' ...
%' iced._be10_al26_quartz.delN26_atoms_g, ' ...
%' iced.base_calculatedages.t_LSDn ' ...
%' from iced.base_sample, iced._be10_al26_quartz, iced.base_calculatedages ' ...
%' where iced.base_sample.id = iced._be10_al26_quartz.sample_id ' ...
%' and iced.base_sample.id = iced.base_calculatedages.sample_unique_id ' ...
%' and iced.base_sample.elv_m is not NULL ' ...
%' and iced._be10_al26_quartz.N10_atoms_g is not NULL ' ...
%' and iced._be10_al26_quartz.N26_atoms_g is not null ' ...
%' and iced._be10_al26_quartz.N26_atoms_g > 1000 ' ...
%' and iced._be10_al26_quartz.N26_atoms_g not like 0 ' ...
% and iced.base_calculatedages.t_LSDn not like 0 ' ...
%' AND iced.base_sample.name NOT LIKE "MH12-47"'];

%% gather the data and organize it into cell arrays that can be used for plotting

samples.table = fetch(dbc,q1);
samples.cell_array = table2array(samples.table(:,[2 3 4 5 6 7]));

% ratio errors is the root of the sum of each error divided by its
% concentration measurement and then all of that multiplied by the
% 26Al-10Be ratio.

samples.error = double((samples.cell_array(:,4)./samples.cell_array(:,2)).*(((samples.cell_array(:,3)./samples.cell_array(:,2)).^2)+((samples.cell_array(:,5)./samples.cell_array(:,4)).^2)).^0.5);

%% The code to maka a figure plotting up all of the samples by elevation vs Al/Be ratio

fig1 = figure(1)
errorbar(samples.cell_array(:,1), (samples.cell_array(:,4)./samples.cell_array(:,2)), samples.error, 'vertical', 'LineStyle','none')
hold on
scatter(samples.cell_array(:,1),...
    (samples.cell_array(:,4)./samples.cell_array(:,2)),...
    'MarkerEdgeColor',[0 0 0], 'MarkerFaceColor', [0 .7 .7], 'SizeData', (samples.cell_array(:,6)./1000),...
    'LineWidth', 0.5)
ylim([0 15])
xlabel('Elevation (m)','FontSize',16)
ylabel('[Al-26] / [Be-10]','FontSize',16)
dim1 = [.8 .9 0 0];
str1 = {['Linear best fit:'], ['m = -0.0002'], ['b = 6.4274'], ...
    ['R^2 = 0.0375']};
annotation('textbox',dim1,'String',str1,'FitBoxToText','on', 'FontSize', 16);
hold on
x1 = samples.cell_array(:,1);
y1=-.0002 * x1 + 6.4274;
plot(x1,y1, "Color", [0 0 0],"LineStyle","-","LineWidth", 2)

%thanks for following along!

---

6) Heinrich Stadials aridity drives glacier retreat in the Mediterranean? This example is a follow up to a paper recently published in Nature Geoscience (Allard et al., 2021) that found that glaciers in the region may have been retreating during Heinrich Stadials due to more arid conditions.

They compiled many moraine and erratic boulder ages from across the Mediterranean, found intervals of erratic boulder deposition during Heinrich events and suggested this as evidence of retreat during Heinrich Stadials.

This is an example of an easily testable hypothesis using ICE-D: Do moraine ages across the Mediterranean more often lie outside of Heinrich Stadial events while erratic boulder ages more often line up within Heinrich Stadial events when compared to a random distribution of both moraine and erratic boulder ages? If yes, this would support the conclusions put forth in Allard et al., 2021. If no, it may bring into question some of the interpretations made in the paper.

The set up would first be to compare a random distribution of both moraine and erratic boulder ages against a North Atlantic record (such as the NGRIP d18O curve) and see how frequently ages line up with Stadials and warm intervals (ie, what % of the time, from x-x ka, do moraine ages line up with Stadial events? What % of the time do random ages line up with warm intervals? And do the same exercise for erratic boulders). Then, run the same exercise for the actual observed ages from the Mediterranean and compare. Is there actual evidence to suggest that moraine ages occur a higher % of the time within warm intervals compared to a random distribution? Is there evidence to suggest that erratic boulder ages occur a higher % of the time within stadial intervals compared to a random distribution? Who knows? Let's find out.

---

7) Identifying regions of possible heavy moraine degradation (using the moraine ages and land degradation models incorporated into the middle layer of calculations) and comparing identified areas of high degradation to geohazards (plate boundaries and areas of high seismic activity). Hypothesis: if geohazards actually present a notable obstacle to moraine dating through moraine degradation, then we should be able to find instances of high moraine degradation coinciding with high seismic activity.